Задача 1. Получить выражение для потенциала и напряженности
электрического поля на оси тонкого равномерно заряженного кольца
радиуса R . Линейная плотность заряда
.
const , показать, что при z R
Считая, что
потенциал поля кольца совпадает в пределе с потенциалом поля точечного
заряда.
1

Ведем цилиндрическую систему координат. Пусть ось совпадает с осью кольца и начало координат с центром кольца, – расстояние от центра коль

Ведем цилиндрическую систему координат. Пусть ось
с осью кольца и начало координат с центром кольца,
от центра кольца до точки наблюдения на оси.
dl
q
2 R
совпадает
– расстояние
Oz
z
dq dl Rd
– элемент длины тонкого кольца
Потенциал для точечного заряда
d
dq
4 0
(z)
2
0
Rd
R 2 z 2 4 0
R
4 0
1
1
R2 z 2
Напряженность поля кольца
d
1
R2 z 2
R
2 0
Ez (z)
1
R2 z 2
d
R
dz 2 0
E z (z) E z (z)
R
(z) (z)
z
2
z
2
3
2

Предельный случай

R
(z)
2 0
R
0
z
R
z
1
2
2
2 0
R z
1
2
R
1
z
z
R
R R
q 1
o
o
2 0 z
z 4 0 z
z
Использовали эквивалентную функцию
1 1
0
2
и
R
q
2
z R
Вывод. В предельном случае при
потенциал поля кольца совпадает с потенциалом поля точечного заряда
3

Задача 2. Получить выражение для напряженности электрического поля, создаваемое тонкой равномерно заряженной дугой окружности радиуса в е

Задача 2. Получить выражение для напряженности электрического
поля, создаваемое тонкой равномерно заряженной дугой окружности
радиуса R
в ее центре О. Линейная плотность заряда
.
4

В силу симметрии и принципа суперпозиции получаем, что

E x 0, E E y e y
Для точечного заряда
dq dl Rd
1
Rd 1
dE y dE cos
cos
cos
2
2
4 0 R
4 0 R
dq
0
0
cos d
Ey 2
sin
2 0 R
2
0 4 R 0
2
5

Задача 3. Найти силу взаимодействия отрезка длиной, равномерно заряженного с линейной плотностью заряда с точечным зарядом, находящимся н

Задача 3. Найти силу взаимодействия отрезка длиной l ,
равномерно заряженного с линейной плотностью заряда
с
точечным зарядом q 0
, находящимся на продолжении отрезка
на расстоянии a от ближайшего его конца.
Пусть ось Ox проходит через отрезок и точечный заряд. Начало
координат совпадает с началом отрезка. Тогда координата точечного
заряда равна
a l
dq dx
.
dq q0
1
dF
4 0 (l a x) 2
q0
q0 a dt
dx
F
2
2
4
4
0 (l a x)
0 l a t
0
l
6

Задача 4. Ось равномерно заряженного диска радиуса совпадает с осью. Центр диска находится в начала координат. Диск заряжен равномерно с по

Задача 4. Ось равномерно заряженного диска радиуса R совпадает
с осью Oz . Центр диска находится в начала координат. Диск
заряжен равномерно с поверхностной плотностью заряда.
Найти потенциал электрического поля, создаваемого диском в точках
оси. Рассмотреть предельный случай:
z R
7

Введем цилиндрическую систему координат

Рассмотрим точечный заряд
d
dq
4 0
dq dS rdrd
rdrd
1
4 0 r 2 z 2
r2 z2
1
2 R rdrd
2 R rdr
(z)
4 0 0 0 r 2 z 2 4 0 0 r 2 z 2
4 0
R2 z2
z2
dt
1/ 2
2 0
t
R z
2
2
z
8

Предельный случай

lim (z) lim
z
z 2
0
2
z
R
1 1
R 2 z 2 z lim
z
z 2
z
0
2
R2
z 1 R 2
R
1
q 1
o
2
2
z 4 0 z 16 0 z
z 2 2 z
z
0
Вывод. При z потенциал электрического поля заряженного
диска совпадает с точностью до константы с потенциалом поля
точечного заряда.
9

10. Задача 5. Найти потенциал ограниченной цилиндрической поверхности радиуса и длиной с зарядом, равномерно распределенным по поверхности.

Задача 5. Найти потенциал ограниченной цилиндрической
поверхности радиуса
R и длиной 2a с зарядом q
равномерно распределенным по поверхности.
,
Способ 1. Нахождение потенциала электрического поля, создаваемого
заряженной цилиндрической поверхностью через потенциал поля
заряженной окружности (тонкого кольца).
qкольца
кольца R
1
1
кольца(z)
, qкольца 2 R кольца
2
2
2
2
4 0 R z
2 0 R z
Рассматриваемая цилиндрическая поверхность – это совокупность
q
заряженных колец с зарядом dq
dz
2a
dq
q
2 R 2a
– заряд цилиндра
dz 2 Rd z
2a
z – координата кольца
10

11. Потенциала поля заряженной цилиндрической поверхности

(z)
a
q / 2a
4
0
a
1
R 2 (z z) 2
dz
a
a z (a z)2 R 2
q
d (z z)
q
ln
8 a 0 a R 2 (z z) 2 8 a 0 a z (a z) 2 R 2
Способ 2. Нахождение потенциала заряженной цилиндрической
поверхности через потенциал поля точечного заряда.
Цилиндрическая поверхность – это совокупность элементарных площадок
поверхности с зарядом
q
q
dq dS
2 R 2a
Rd dz
4 a
d dz
q 2 a
d dz
(z)
4 0 4 a 0 a R 2 (z z) 2

Точечным зарядом называется заряженное тело, размерами которого можно пренебречь по сравнению с расстояниями от этого тела до других тел, несущих электрический заряд.

Закон Кулона: Сила взаимодействия двух неподвижных точечных зарядов пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между ними. Направление силы совпадает с соединяющей эти заряды прямой.

где k – коэффициент пропорциональности,q 1 иq 2 – величины взаимодействующих зарядов,r – расстояние между ними,e 12 – единичный вектор направленный от заряда1 к заряду2 ,F 12 – сила, действующая на заряд2 со стороны заряда1 .

Коэффициент k определяется следующим образом:

,

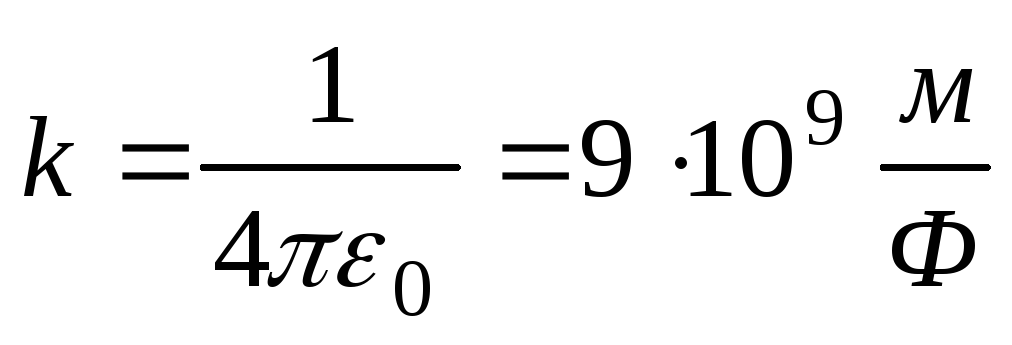где  0 = 8,85 10 -12 Ф/м – электрическая постоянная.

Напряженность поля , создаваемого точечным зарядомq прямо пропорциональна заряду и обратно пропорциональна квадрату расстояния от заряда до данной точки поля:

,

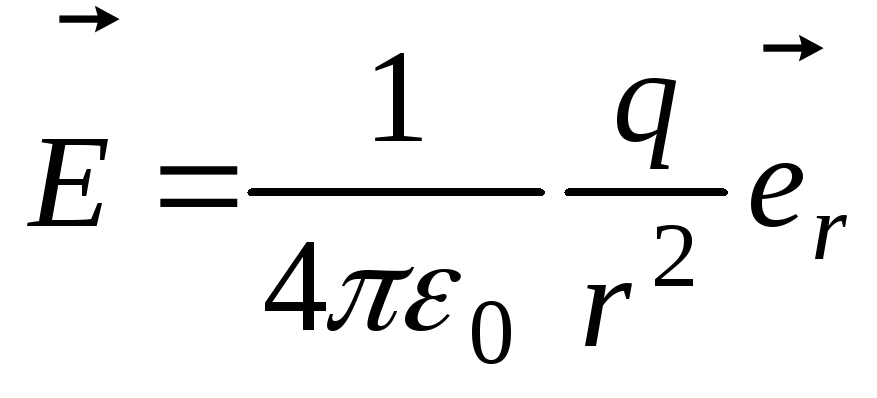вектор направлен вдоль прямой, проходящей через заряд и данную точку поля, от заряда, если он положителен, и к заряду, если он отрицателе.

Принцип суперпозиции : напряженность поля системы зарядов равна векторной сумме напряженностей полей, создаваемых каждым зарядом в отдельности:

.

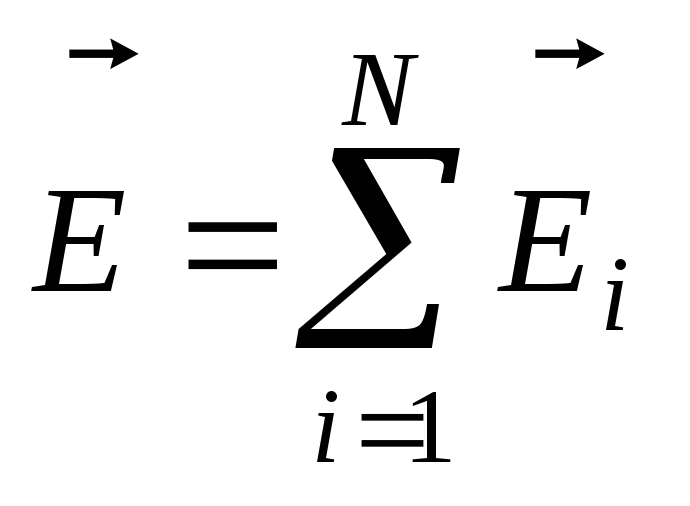Потенциал поля точечного заряда:

.

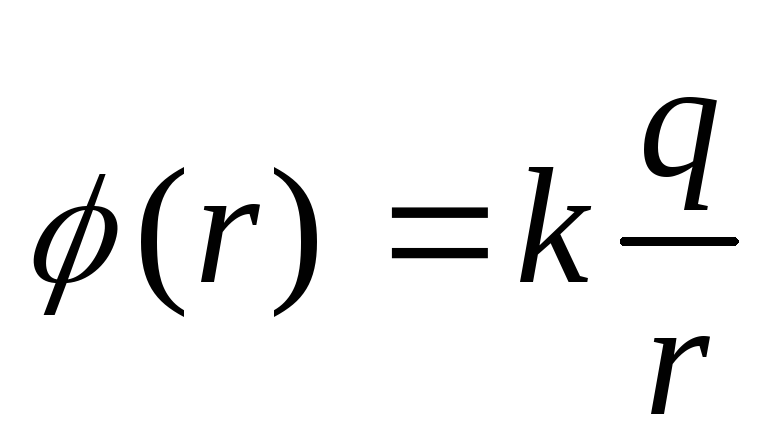По принципу суперпозиции потенциал системы точечных зарядов равен:

.

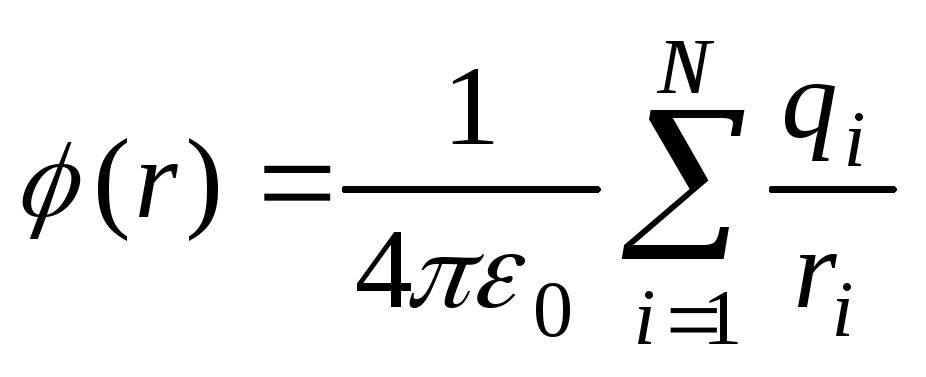II. Примеры решения задач

Пример 1.1. Тонкая проволока, представляющая по форме четверть кольца радиусаR , заряжена равномерно зарядомq . Найти напряженность поля в центре кривизны.

Решение.

Выбираем на кольце элементарный заряд

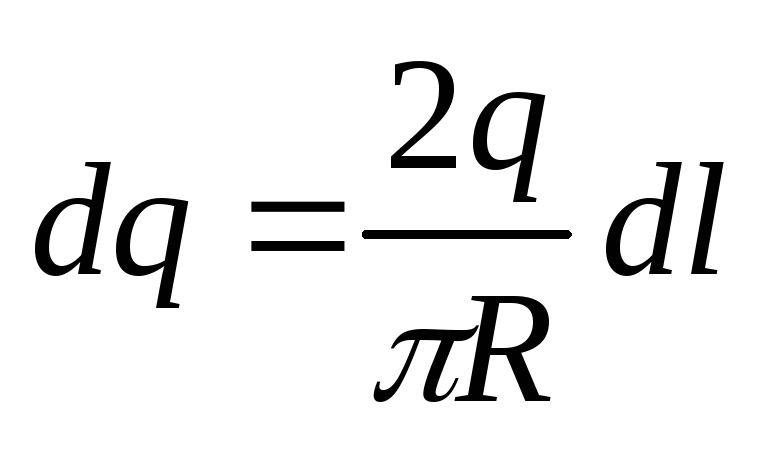, где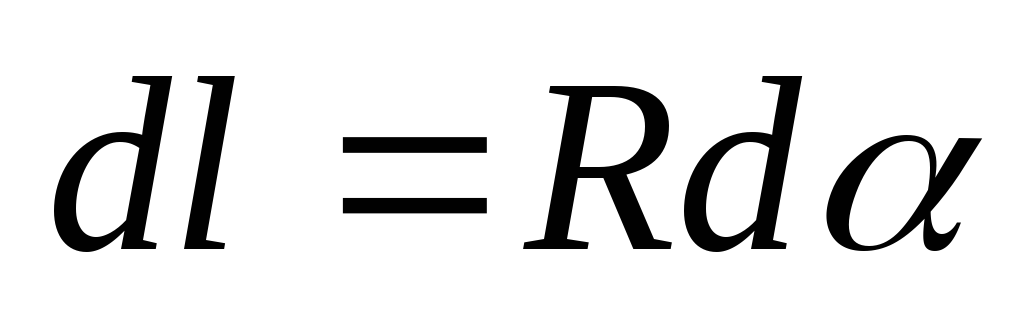

иd  - угол под которым из центра кривизны виден элементdl . Напряженность поля, создаваемого этим элементарным зарядом, равна:

.

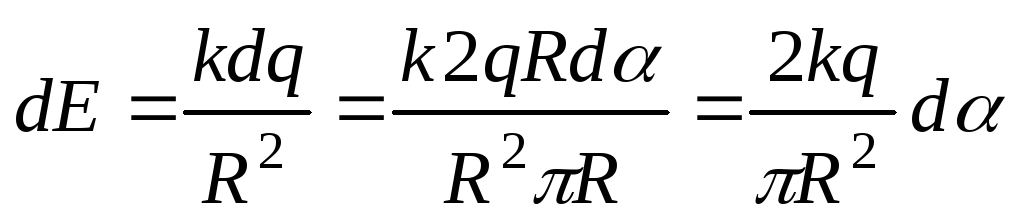Введем оси координат и находим проекции напряженности поля на выбранные оси:

.

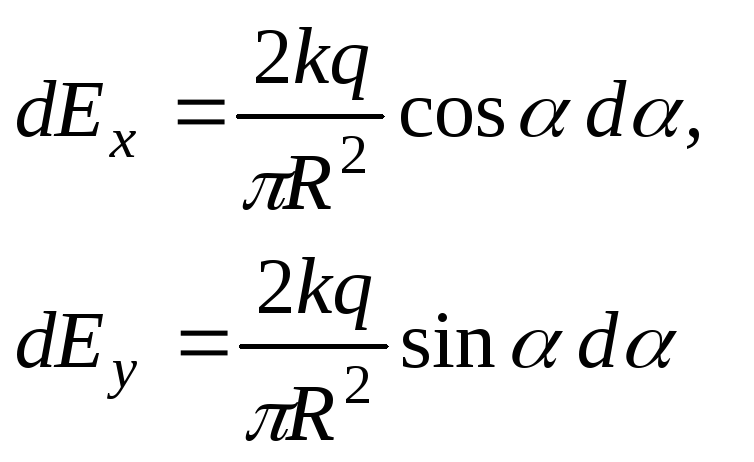Тогда суммарная напряженность будет равна:

.

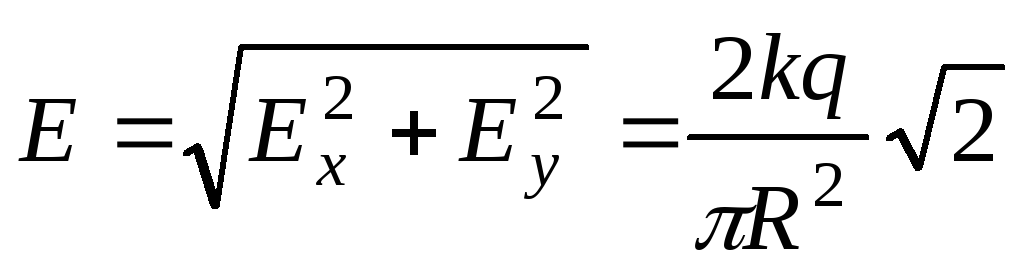Вектор напряженности направлен под углом 45к осих .

Пример 1.2 Находящейся в вакууметонкий прямой стержень длины 2а заряжен равномерно с зарядомq . Найти модуль напряженности электрического поля как функцию расстоянияr от центра стержня до точки прямой, совпадающей с осью стержняr >a .

Решение.

Вводим обозначения:

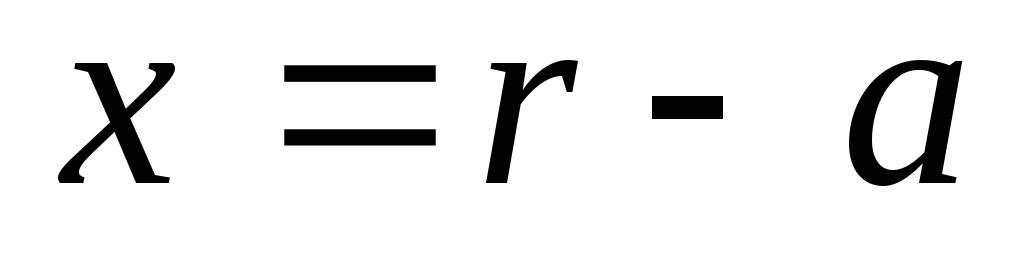. Выделим на стержне элементdl , заряд этого элемента равен: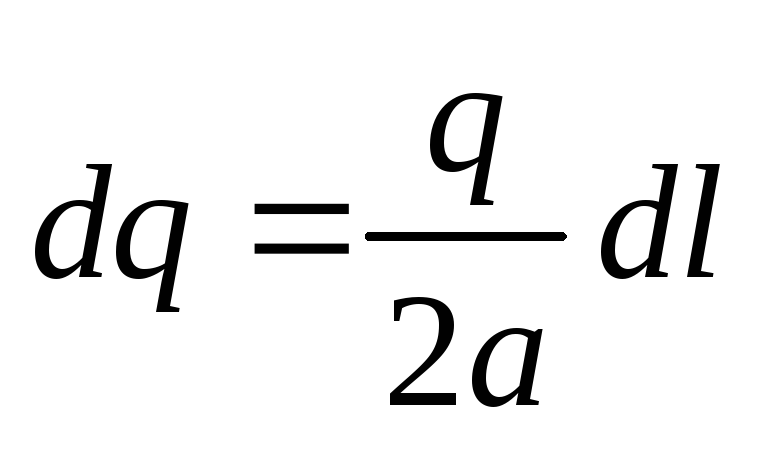

. Напряженность поля, создаваемого в точке наблюдения таким зарядом равна:

,

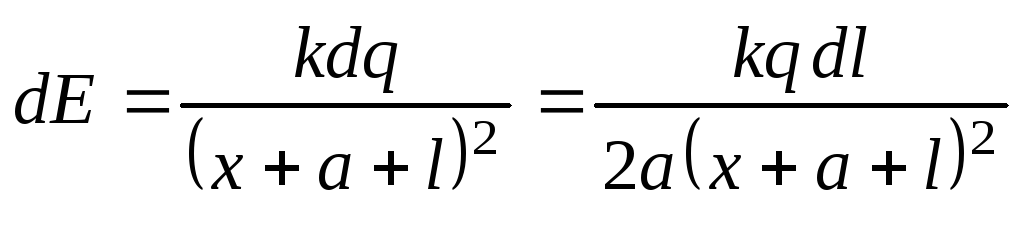где l – расстояние от центра стержня до элементаdl . Поле, создаваемое всем стерж7нем будет равно:

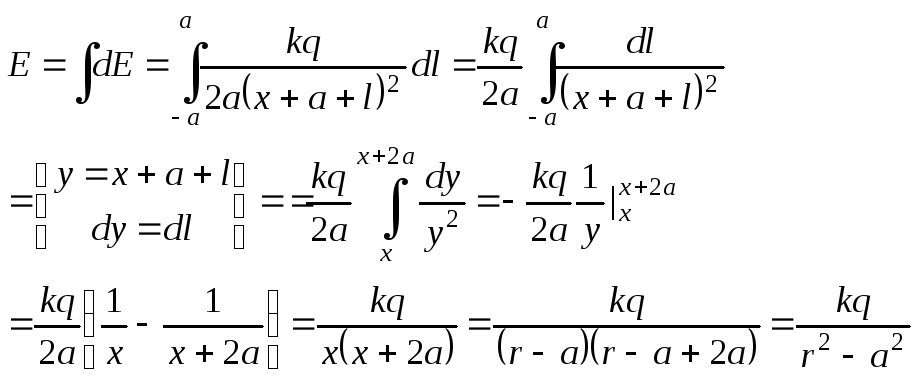
III. Задачи для самостоятельного решения

1.1. Кольцо радиусаRимеет зарядq. Найти модуль напряженности электрического поля на оси кольца как функцию расстоянияLдо его центра.

Ответ: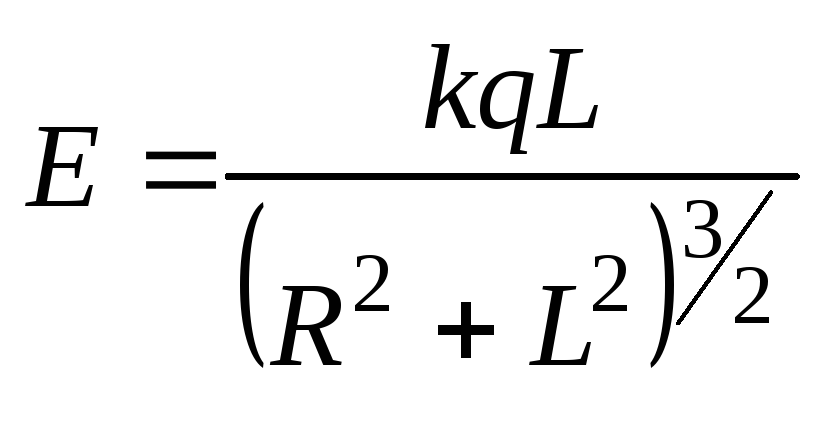

.

1.2. Тонкая проволока, представляющая по форме кольцо радиусаR, заряжена равномерно зарядомq. Найти напряженность поля в центре кольца.

Ответ: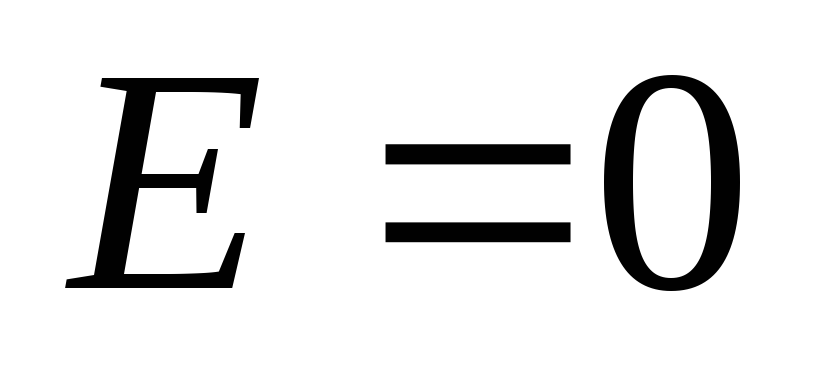

.

1.3. Тонкое полукольцо радиусаRимеет положительный зарядq. Найти напряженность в центре кривизны этого полукольца.

Ответ: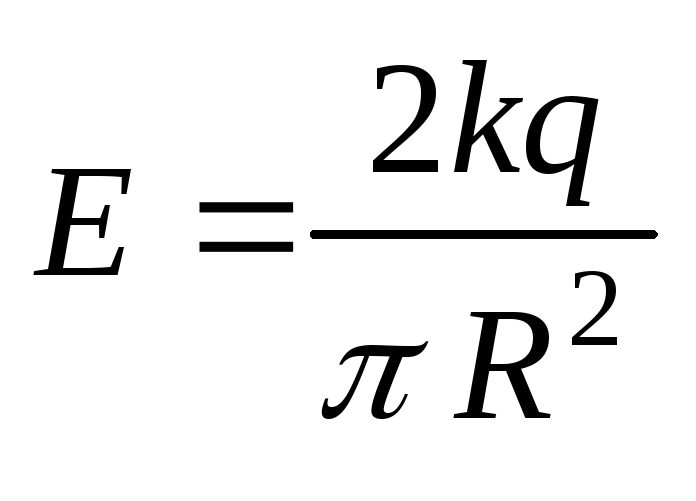

.

1.4. Тонкая проволока, представляющая по форме три четверти кольца радиусаR, заряжена равномерно зарядомq. Найти напряженность поля в центре кривизны.

Ответ: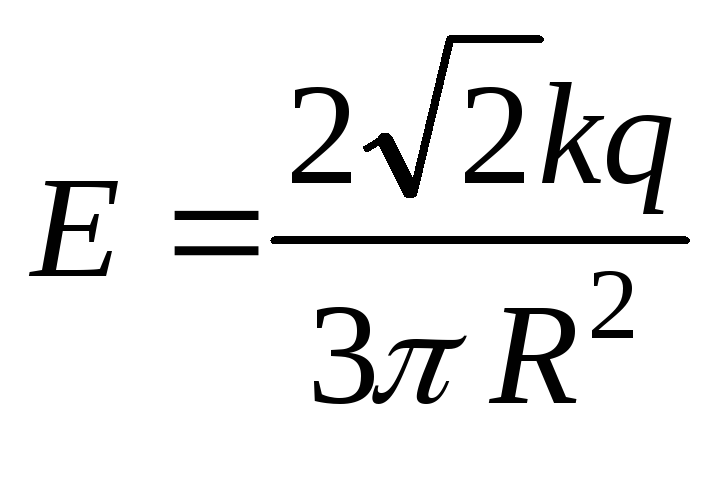

.

1.5.

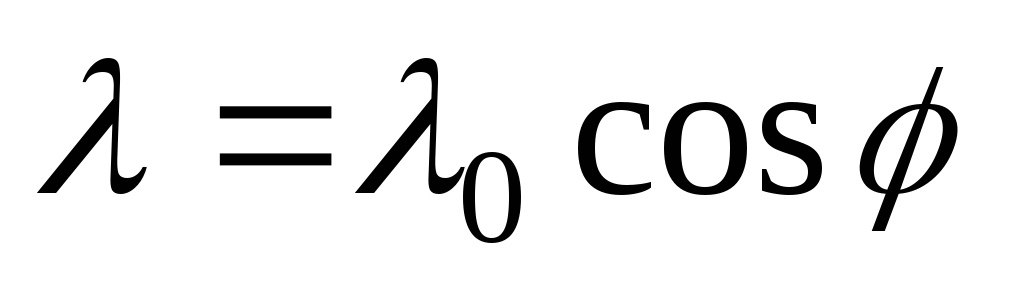, где

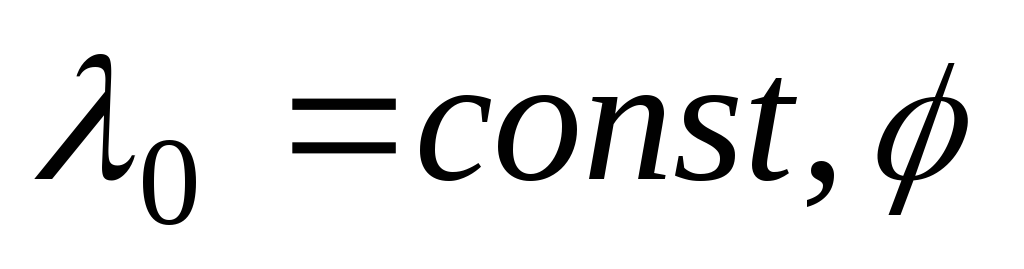- азимутальный угол. Найти напряженность: а) в центре кольца, б) на оси кольца в зависимости от расстоянияL.

Ответ:

.

1.6. Тонкое непроводящее кольцо радиусаRзаряжено с линейной плотностью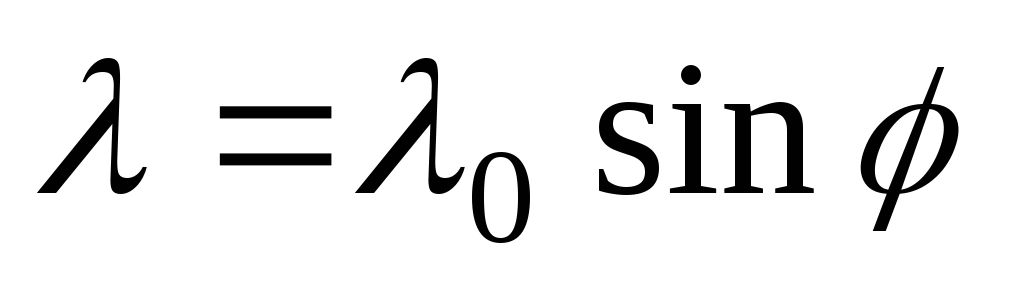

, где

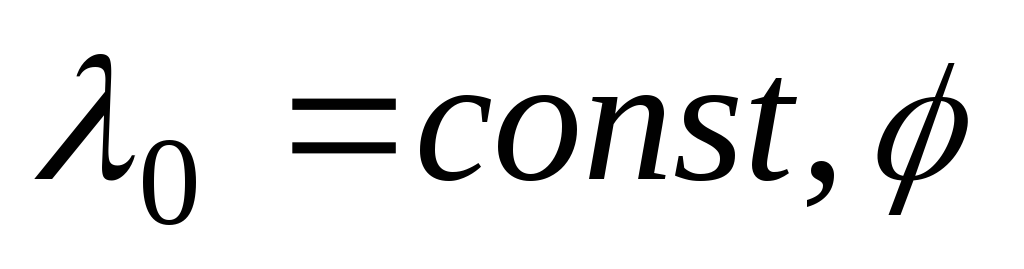- азимутальный угол. Найти напряженность в центре кольца.

Ответ: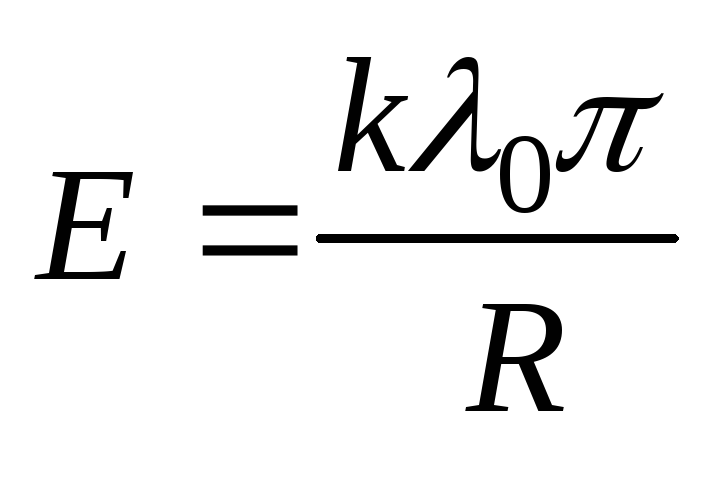

.

1.7. Очень длинная прямая нить заряжена с линейной плотностью. Найти модуль и направление напряженности электрического поля в точке, которая отстоит от нити на расстояниеLи находится на перпендикуляре к нити.

Ответ: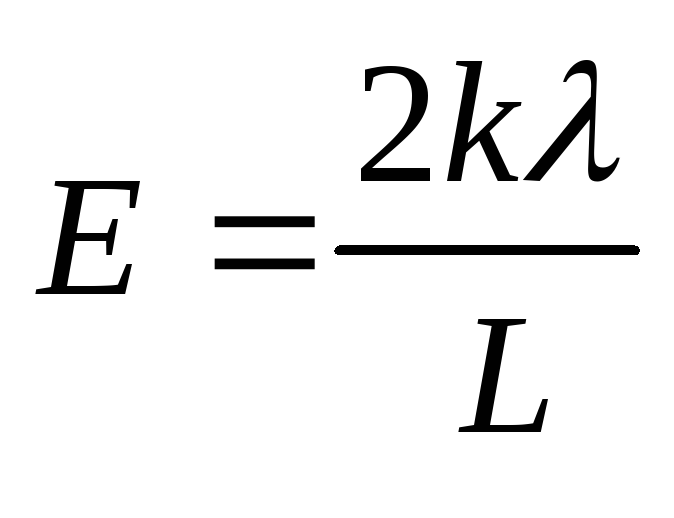

.

1.8. Очень длинная прямая нить заряжена с линейной плотностью. Найти модуль и направление напряженности электрического поля в точке, которая отстоит от нити на расстояниеLи находится на перпендикуляре к нити, проходящем через один из ее концов.

Ответ: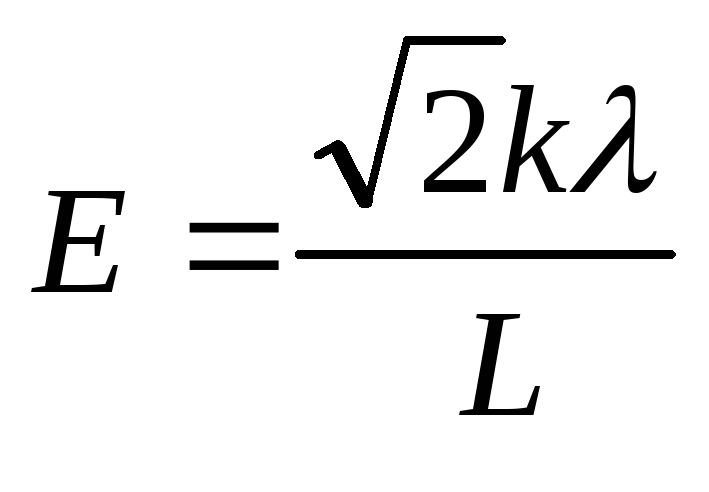

.

1.9. Тонкий прямой стержень длины 2а равномерно заряжен с линейной плотностью. НайтиE(L), гдеL-расстояние от центра стержня до точки прямой, перпендикулярной стержню и проходящей через его центр.

Ответ: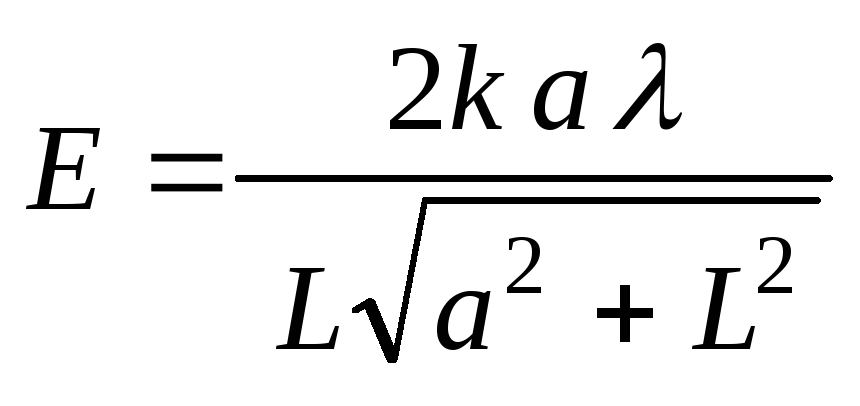

.

1.10. Тонкий прямой стержень длины 2а равномерно заряжен с линейной плотностью. НайтиE(L), гдеL-расстояние от центра стержня до точки прямой совпадающей с осью стержня, если

.

Ответ: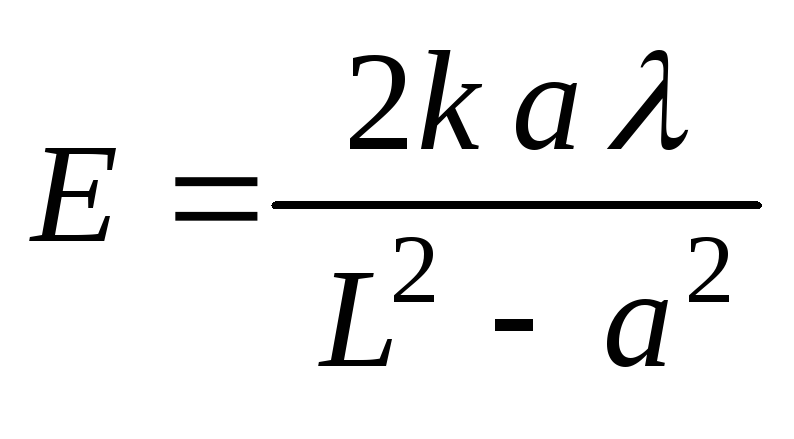

.

1.11. Равномерно заряженная нить, на единицу длины которой приходится заряд, имеет конфигурацию, показанную на рис.1.3. Радиус закругленияRгораздо меньше длинны нити. Найти модуль напряженности электрического поля в точке О.

Ответ: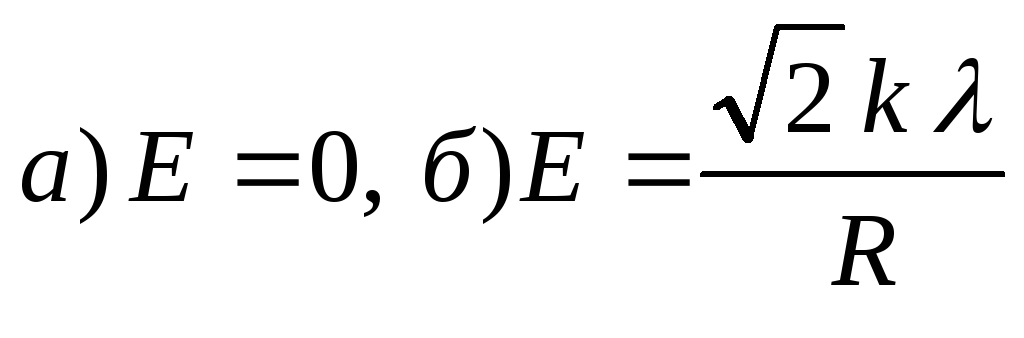

.

1.12. Находящаяся в вакууме тонкая пластинка радиусаRравномерно заряжена с поверхностной плотностью. Найти модуль напряженности электрического поля на оси пластинки как функцию расстоянияLот ее центра.

Ответ: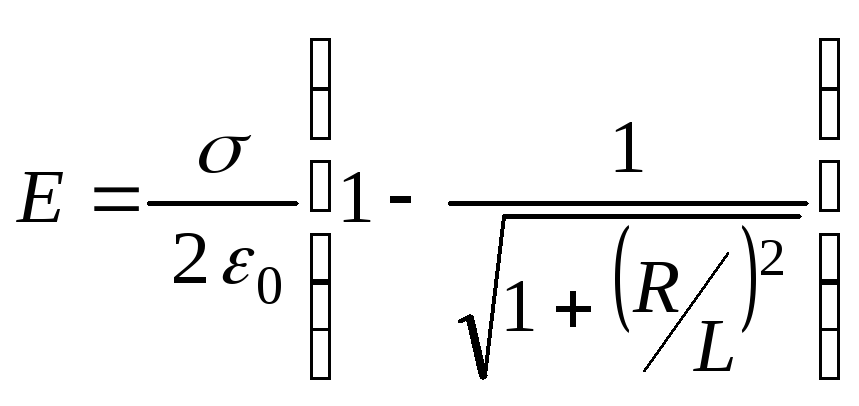

.

1.13 . Плоское кольцо, внутренний радиус которого а, внешний в, заряжено с поверхностной плотностью. Найти модуль напряженности электрического поля на оси кольца как функцию расстоянияLот его центра.

О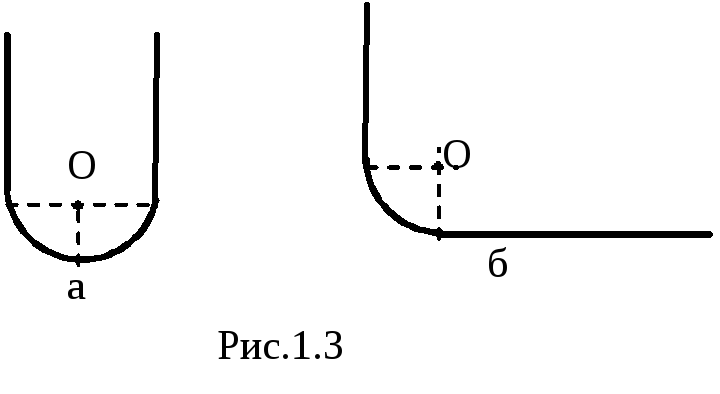

твет: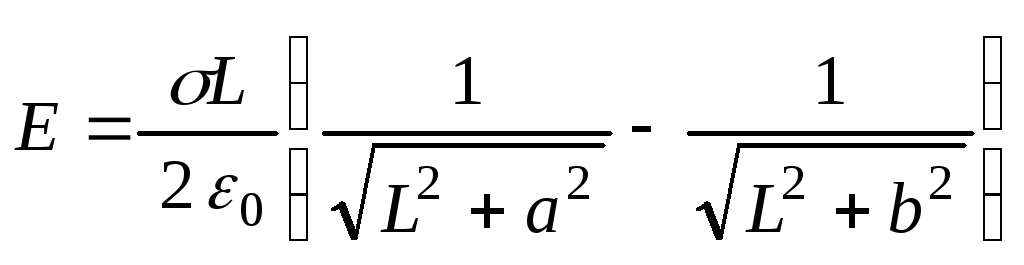

.

1.14. Зарядqраспределен равномерно по объему шара радиусаR. Найти потенциал:

а) в центре шара  0 , б) внутри шара(r), в) вне шара(r), гдеr- расстояние от центра шара.

1.15. Потенциал поля внутри заряженного шара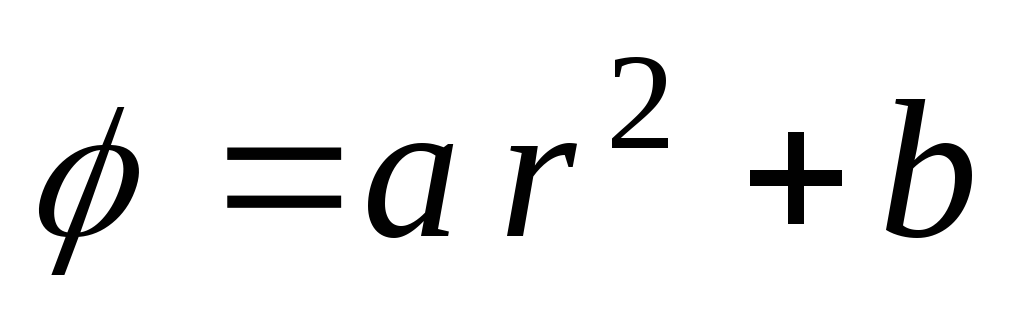

, гдеа иb – постоянные. Найти зависимость объемной плотности заряда(r) от расстояния от центра шара.

Ответ: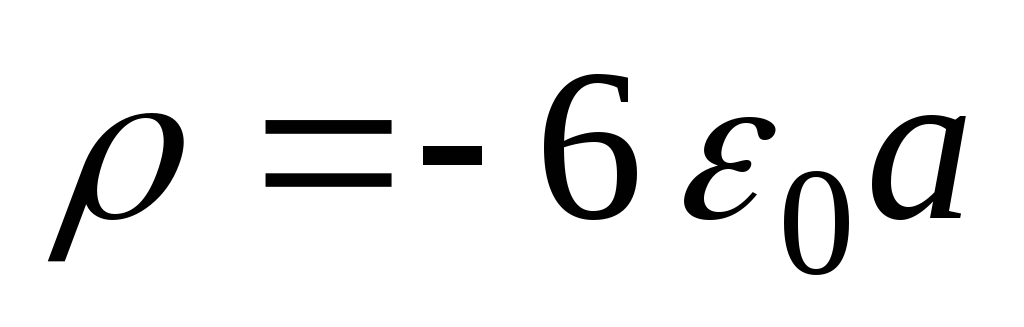

.

1.16. По сфере радиусаRравномерно распределены заряды с поверхностной плотностьюНайти потенциал в зависимости от расстояния до центра сферы.

Ответ: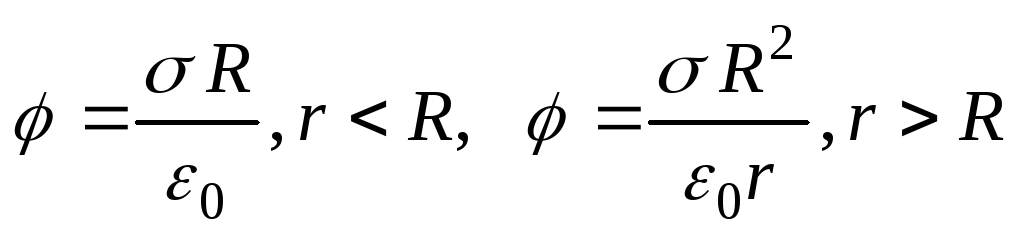

.

1.17 . Плоское кольцо, внутренний радиус которогоа , внешнийb , заряжено с поверхностной плотностью. Найти потенциал в центре кольца.

Ответ: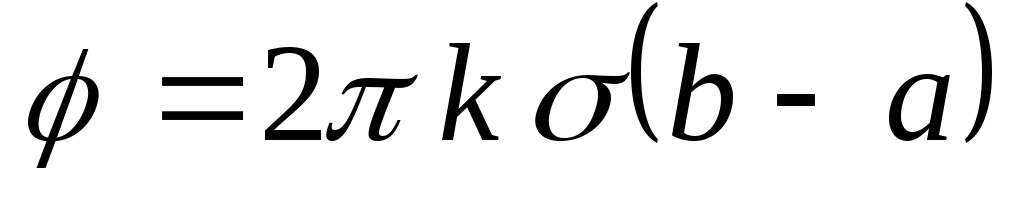

.

1.18. Находящаяся в вакууме тонкая пластинка радиусаRравномерно заряжена с поверхностной плотностью. Найти потенциал электрического поля на оси пластинки как функцию расстоянияLот ее центра.

Ответ: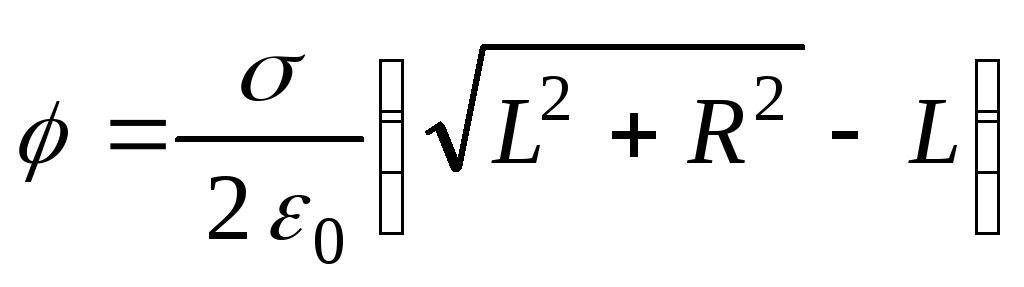

.

1.19 . Две длинные одноименно заряженные нити расположены на расстоянии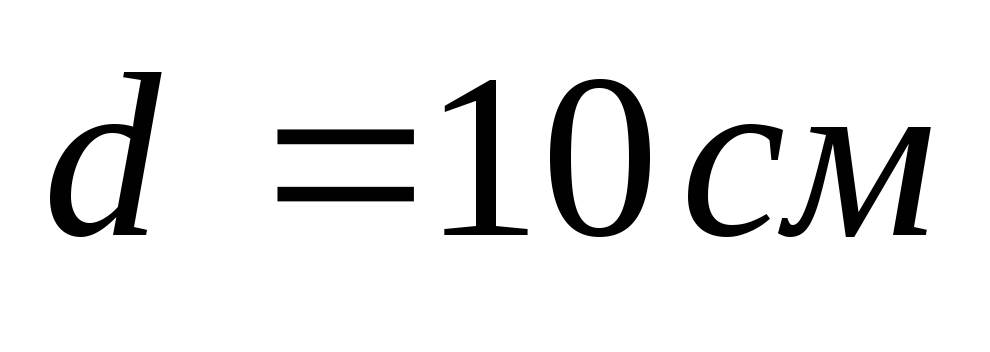

друг от друга. Линейная плотность заряда на нитях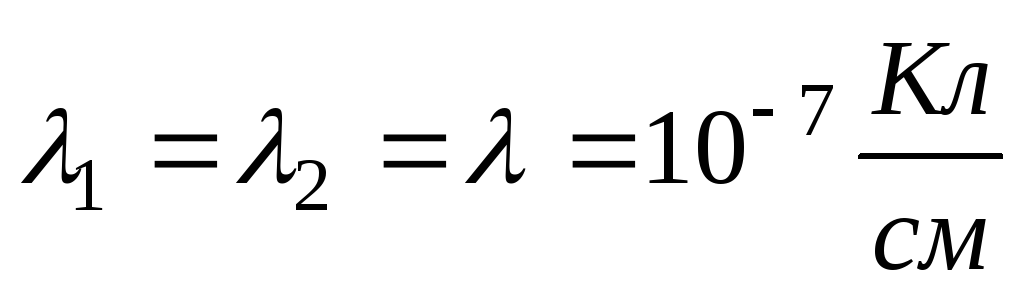

. Найти величину и направление напряженности результирующего электрического поля в точке, находящейся на расстоянии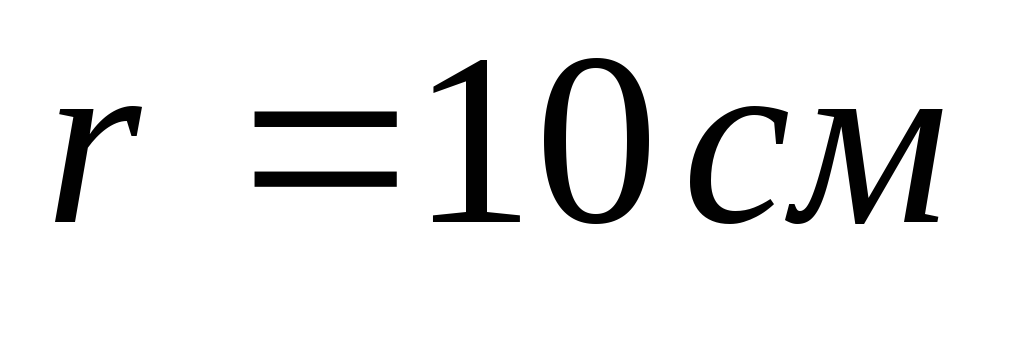

от каждой нити.

Ответ: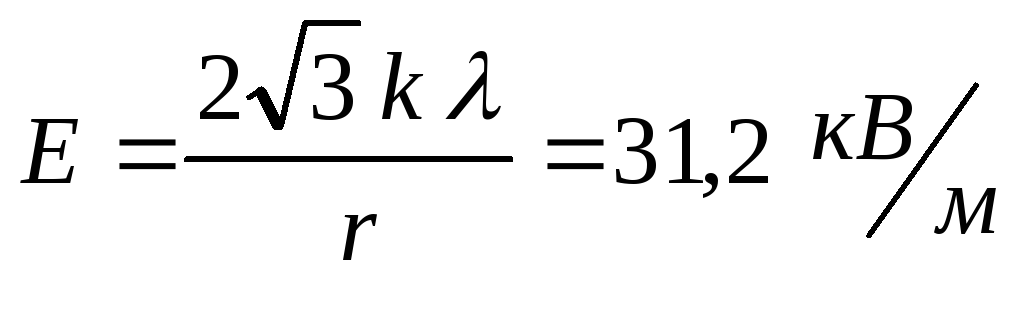

.

Пример расчета напряженности Электрического поля равномерно заряженного тонкого кольца

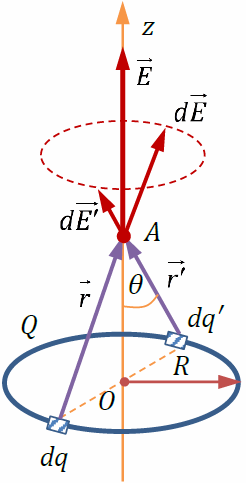По тонкому кольцу равномерно распределён заряд Q > 0. Находим напряжённость электрического поля в точке A на оси кольца (OA = z ). Разобьём кольцо на точечные заряды dq (на рисунке показаны два малых заряда dq и dq′ , равные по модулю и расположенные диаметрально противоположно). По принципу суперпозиции полей – где dE - напряжённость электрического поля малого заряда dq .

Векторы напряжённости электрического поля каждого из этих зарядов одинаковы по модулю и направлены так, что концы этих векторов образуют конус с вершиной в точке A (штриховой линией показано основание этого конуса). Проекции этих векторов на плоскость кольца компенсируются, поэтому суммарный вектор направлен вдоль оси z : E (при z > 0). Вычислим Ez . Напряжённость поля точечного заряда:

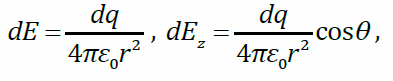
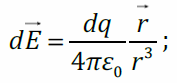Величины r иθ (угол) одинаковы для всех элементов dq :

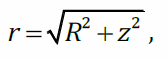
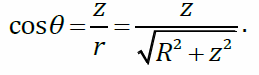подставим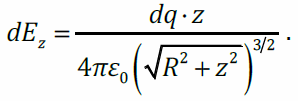

В этом выражении все величины – постоянные, кроме dq. Проинтегрируем по q:

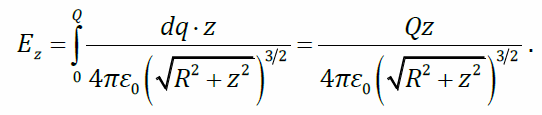
Поток вектора напряженности. Теорема Остроградского-Гауса для электростатического поля в вакууме. Применение теоремы к расчету напряженности поля. Пример: поле бесконечно большой равномерно заряженной плоскости.

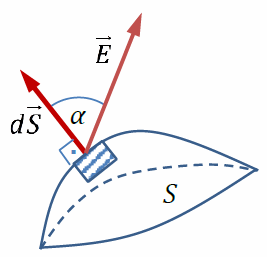Введем новую физическую величину, характеризующую электрическое поле – поток вектора напряженности электрического поля (Φ).

Элементарный поток направлен по внешней нормали к малому участку dS (Если поверхность S не замкнута, то выбор одного из двух направлений нормали произволен, при этом направление нормали для всех участков dS должно быть одинаковым)

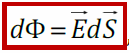
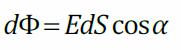
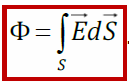
Полный поток вектора сквозь поверхность S E

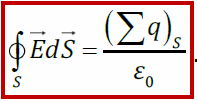
Теорема Остроградского-Гаусса для: поток вектора напряжённости электрического поля сквозь произвольную замкнутую поверхность равен алгебраической сумме зарядов, охваченной этой поверхностью, делённой на ε 0:

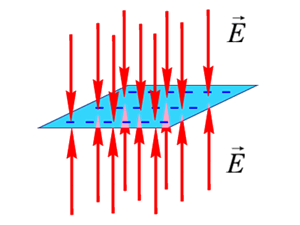
Поле равномерно заряженной бесконечной плоскости :
, где - поверхностная плотность заряда.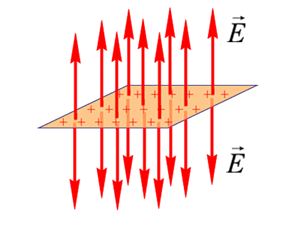

Работа сил электростатического поля по перемещению заряда. Потенциал электростатического поля. Связь между напряженностью поля и потенциалом. Понятие градиента. Методы расчета потенциала. Пример: потенциал на оси равномерно заряженного кольца.

I уравнение Максвелла для электростатического поля умножим на пробный заряд q 0:

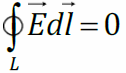
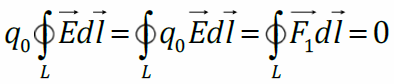
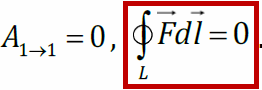Работа электростатического поля по перемещению пробного заряда по произвольной замкнутой траектории равна нулю. Это означает, что электростатическое поле потенциально. Потенциальная энергия заряженной частицы в электростатическом поле равна работе внешних сил при перемещении этой частицы из точки, где потенциальная энергия принята равной нулю, в данную точку, или работе поля при этом перемещении: .Потенциальная энергия – характеристика и поля, и заряда: