Определение: Кинетической энергией тела называется энергия его поступательного движения.

Если внешняя сила действует на покоящееся тело, последнее приобре­тает некоторую скорость и способно само совершить работу. Этот запас работы и называется кинетической энергией тела. Запишем уравнение движения материальной точки:

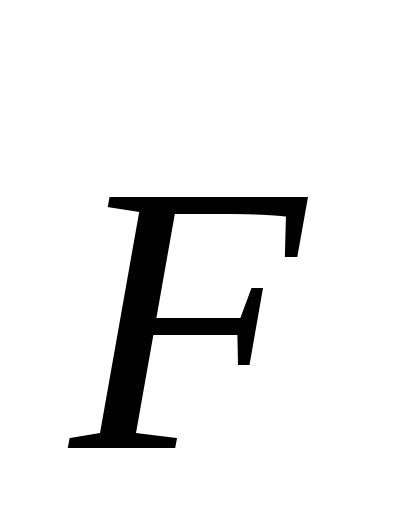
где  результирующая сила. Умножим уравнение движения скалярно на

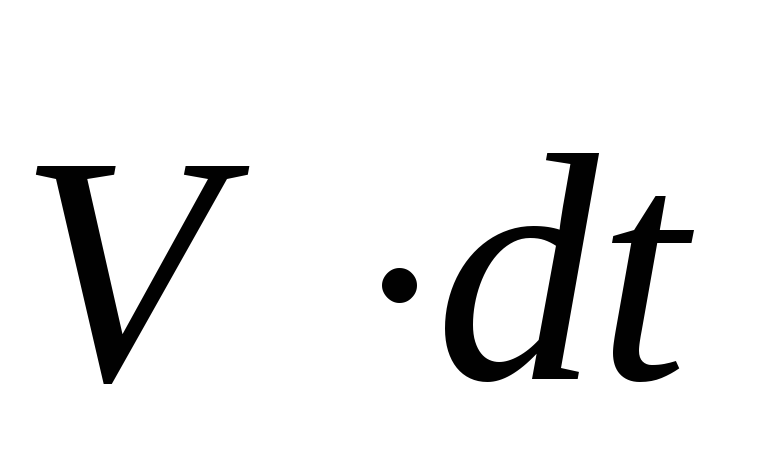, тогда

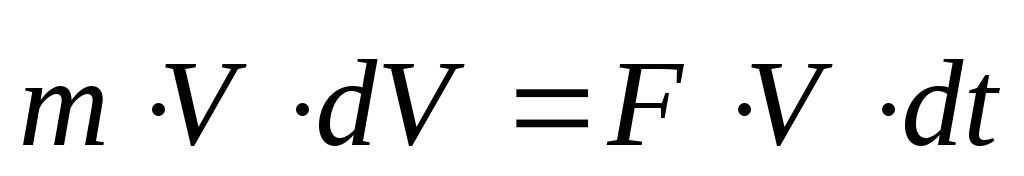
В правой части уравнения мы получили элементарную работу , в ле­вой - выражение, которое можно преобразовать к виду полного дифференциала:

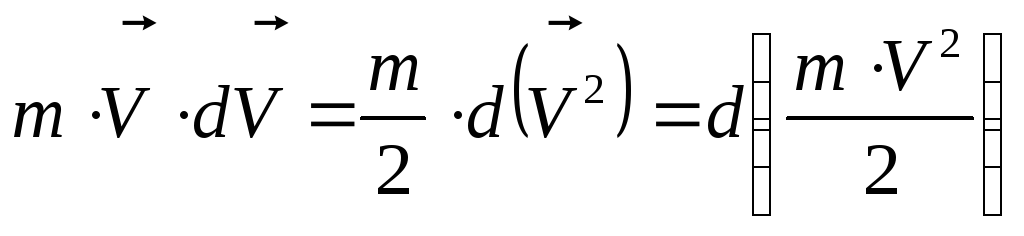
В результате имеем

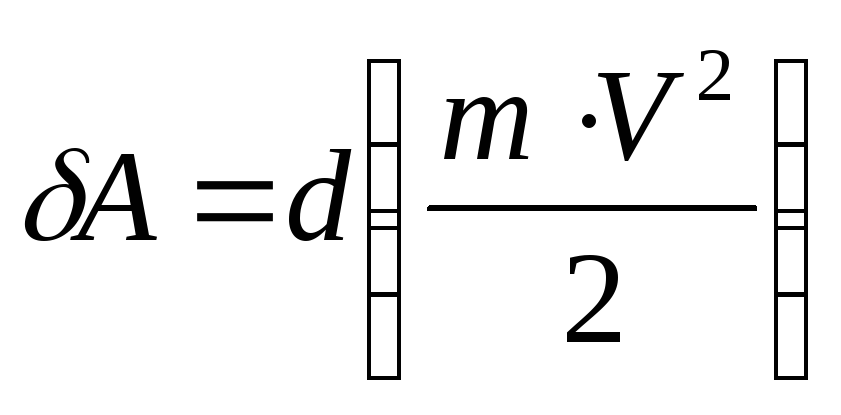, т.е. элементарная работа, совершенная силой,равна приращению величины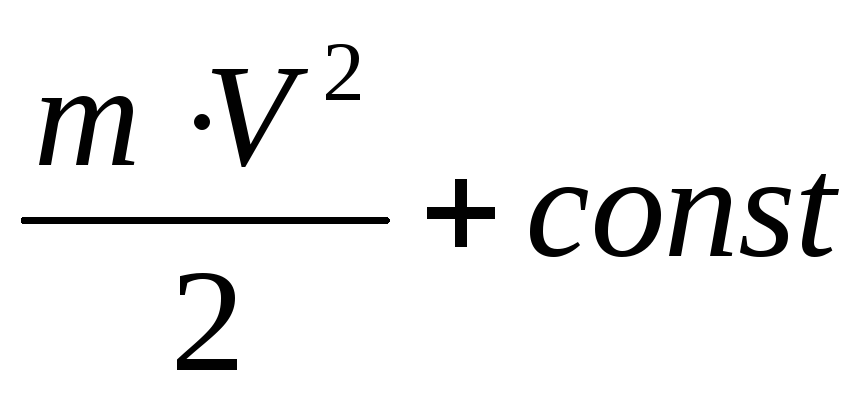

, определяемой с точностью до произвольной постоянной. Получается, что сила совершает некоторую работу, и на такое же количество возрастает кинетическая энергия тела (обычное обозначениеТ или W кин. ). При отрицательной ра­боте силы кинетическая энергия тела убывает: энергия расходуется на преодоление действующей силы. Обычно считают, что покоящееся тело кинетической энергией не обладает, так что произвольную постоянную полагают равной нулю:

.

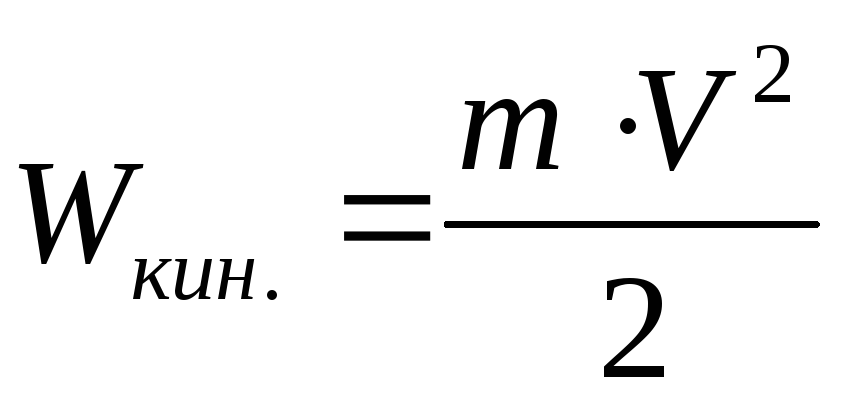§17.Потенциальная энергия.

Определение: Потенциальной энергией называется часть энергии механической системы, зависящей только от её конфигурации, т.е. от взаимного расположения всех частиц системы и, от расположения во внешнем потенциальном поле.

Убыль потенциальной энергии при перемещении системы из произвольного положения «1» в другое положение «2» измеряется той работой А 12 , которую совершают при этом все потенциальные: внутренние и внешние, силы, действующие на систему:

U (1)  U (2) = А 12 или U =  А 12 ,

где  U = U (2)  U (1) изменения потенциальной энергии механической системы,

U (1), U (2) значения потенциальной энергии механической системы в положениях «1» и «2».

Соответственно, работа потенциальных сил при малом изменении конфигурации системы  А =  dU .

Данные соотношения справедливы для случая стационарного (не зависящего от времени) внешнего потенциального поля. Для простейшего случая, нахождения материальной точки во внешнем потенциальном поле, сила с которой это поле действует на точку, вычисляется по формуле:

где

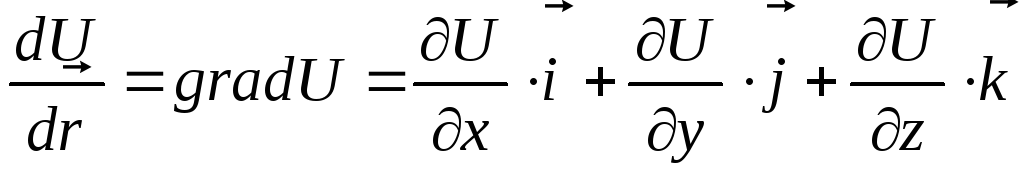называется градиентом скалярной функции (в данном случаепотенциальной энергии). Градиентэто векторная величина, направленная в сторону роста значений функцииU . В приведённой формуле фигурирует знак «», который указывает, что сила направлена в сторону убыли значений функцииU .

Обратное соотношение, позволяющее по известному выражению потенциальной силы, вычислить значение потенциальной энергии, очевидно,

.

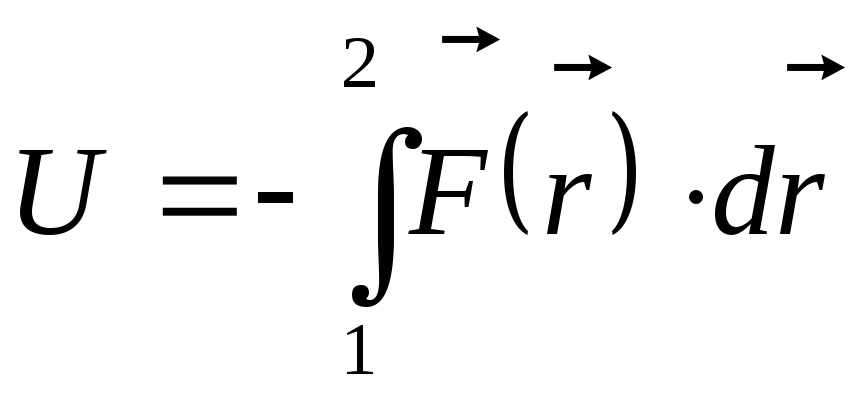Приведённая формула даёт возможность определения явных выражений потенциальной энергии для частных случаев. При вычислении данного интеграла, один из пределов стремятся выбрать таким, чтобы потенциальная энергия в рассматриваемой точке была равна нулю.

Пример №1.

Сила гравитационного взаимодействия двух тел равна

,

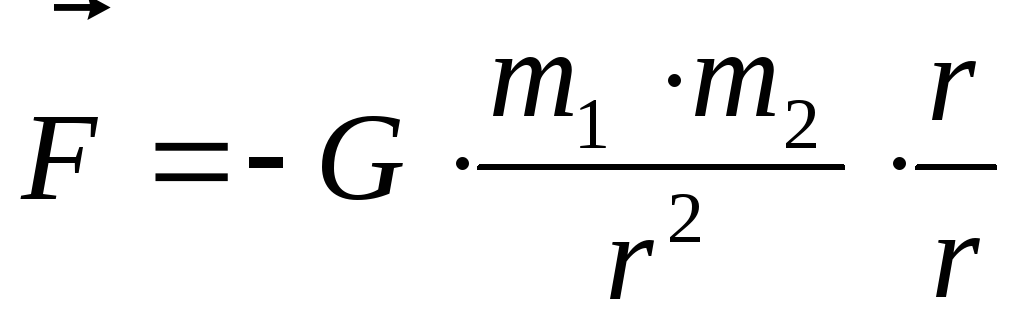С понятием работы тесно связано другое фундаментальное физическое понятие – понятие энергии. Поскольку в механике изучается, во-первых, движение тел, а во-вторых, взаимодействие тел между собой, то принято различать два вида механической энергии: кинетическую энергию , обусловленную движением тела, и потенциальную энергию , обусловленную взаимодействием тела с другими телами.

Кинетической энергией механической системы называют энергию, з ависящую от скоростей движения точек этой системы.

Выражение для кинетической энергии можно найти, определив работу равнодействующей силы, приложенной к материальной точке. На основании (2.24) запишем формулу для элементарной работы равнодействующей силы:

Так как

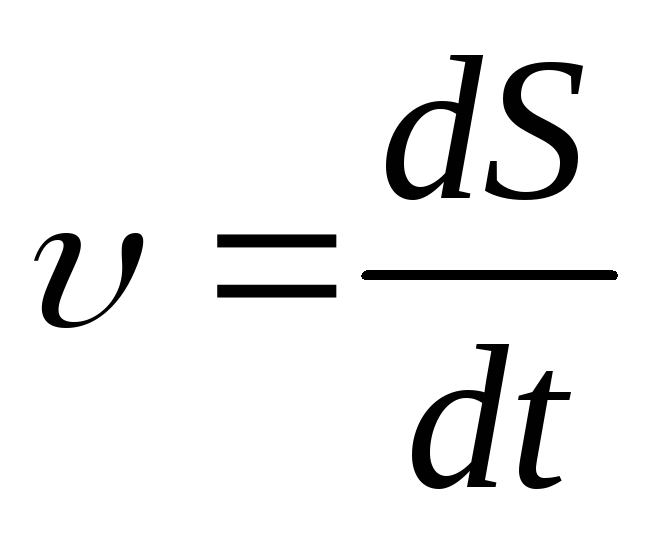, то dА = mυdυ. (2.25)

Чтобы найти работу равнодействующей силы при изменении скорости тела от υ 1 до υ 2 проинтегрируем выражение (2.29):

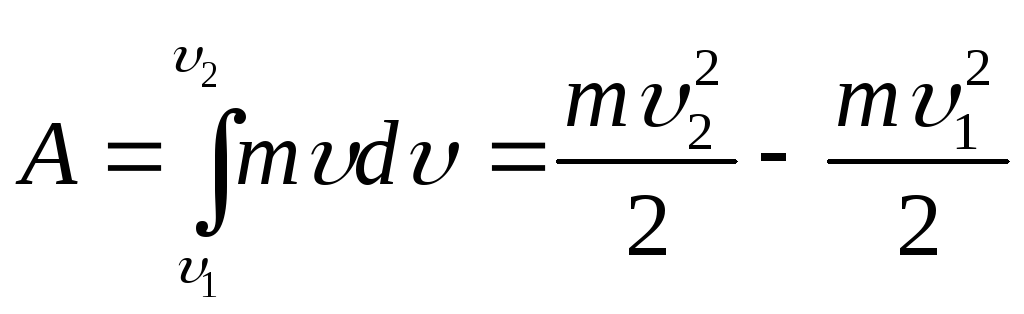(2.26)

Так как работа - мера передачи энергии от одного тела другому, то на

основании (2.30) запишем, что величина 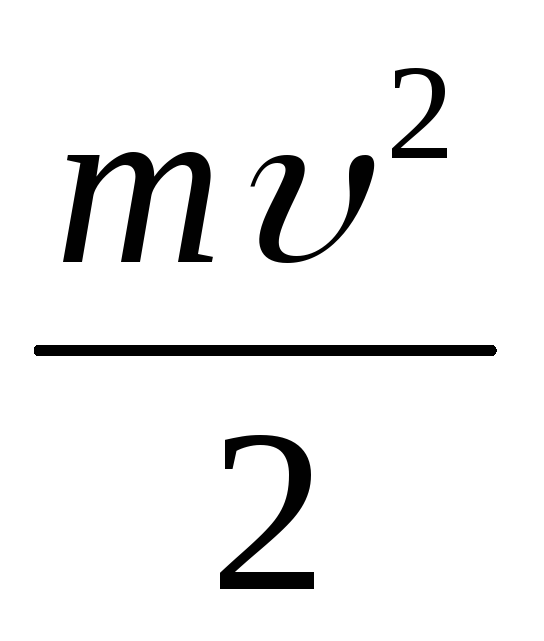есть кинетическая энергия

тела:

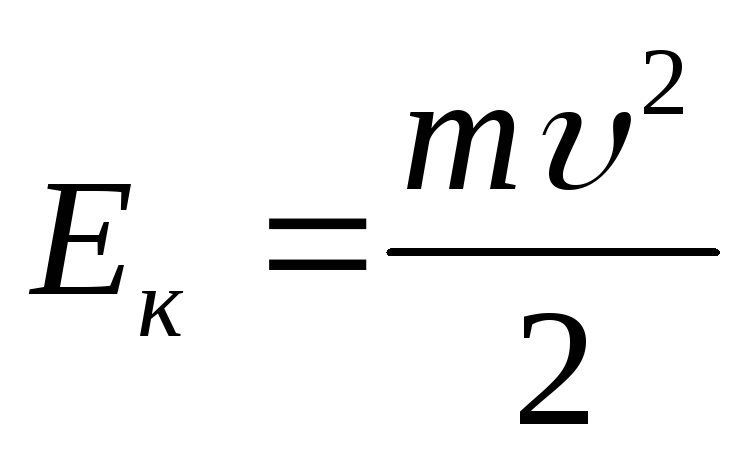откуда вместо (1.44) получаем

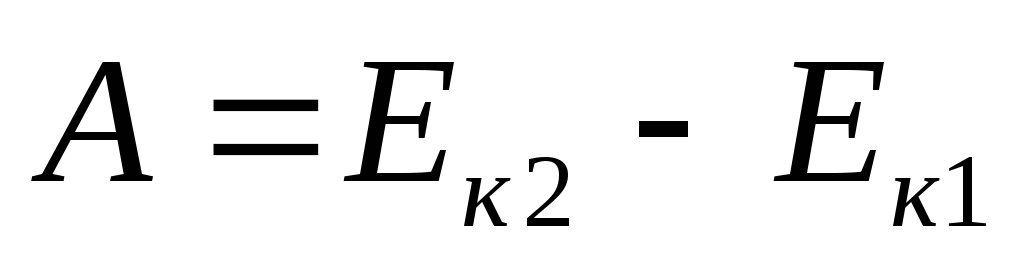(2.27)

Теорему, выраженную формулой (2.30) принято называть теоремой о кинетической энергии . В соответствии с ней работа сил, действующих на тело (или систему тел), равна изменению кинетической энергии этого тела (или системы тел).

Из теоремы о кинетической энергии следует физический смысл кинетической энергии : кинетическая энергия тела равна работе, которую оно способно совершать в процессе уменьшения своей скорости до нуля. Чем больше «запас» кинетической энергии у тела, тем большую работу оно способно совершить.

Кинетическая энергия системы равна сумме кинетических энергий материальных точек, из которых эта система состоит:

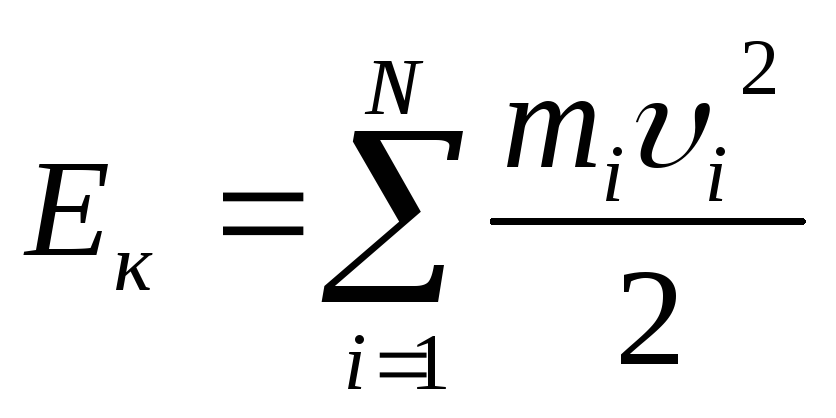(2.28)

Если работа всех сил, действующих на тело, положительна, то кинетическая энергия тела возрастает, если работа отрицательна, то кинетическая энергия убывает.

Очевидно, что элементарная работа равнодействующей всех приложенных к телу сил будет равна элементарному изменению кинетической энергии тела:

dА = dЕ к. (2.29)

В заключение заметим, что кинетическая энергия, как и скорость движения, имеет относительный характер. Например, кинетическая энергия пассажира, сидящего в поезде, будет разной, если рассматривать движение относительно полотна дороги или относительно вагона.

§2.7 Потенциальная энергия

Вторым видом механической энергии является потенциальная энергия – энергия, обусловленная взаимодействием тел.

Потенциальная энергия характеризует не любое взаимодействие тел, а лишь такое, которое описывается силами, не зависящими от скорости. Большинство сил (сила тяжести, сила упругости, гравитационные силы и т.д.) именно таковы; исключением являются лишь силы трения. Работа рассматриваемых сил не зависит от формы траектории, а определяется лишь её начальным и конечным положением. Работа таких сил на замкнутой траектории равна нулю.

Силы, работа которых не зависит от формы траектории, а зависит лишь от начального и конечного положения материальной точки (тела) называют потенциальными или консервативными силами .

Если тело взаимодействует со своим окружением посредством потенциальных сил, то для характеристики этого взаимодействия можно ввести понятие потенциальной энергии.

Потенциальной называют энергию, обусловленную взаимодействием тел и зави­сящую от их взаимного расположения.

Найдем потенциальную энергию тела, поднятого над землей. Пусть тело массой m равномерно перемещается в гравитационном поле из положения 1 в положение 2 по поверхности, сечение которой плоскостью чертежа показано на рис. 2.8. Это сечение является траекторией материальной точки (тела). Если трение отсутствует, то на точку дейст­вуют три силы:

1) сила N со стороны поверхности нормально поверхности, работа этой силы равна нулю;

2) сила тяжести mg, работа этой силы А 12 ;

3) сила тяги F со стороны некоторого движущего тела (двигатель внутреннего сгорания, электродвигатель, человек и т. п.); работу этой силы обозначим А T .

Рассмотрим работу силы тяжести при перемещении тела вдоль наклонной плоскости длиной ℓ (рис. 2.9). Как видно из этого рисунка, работа равна

А" = mgℓ соsα = mgℓ соs(90° + α) = - mgℓ sinα

Из треугольника ВСD имеем ℓ sinα = h, по­этому из последней формулы следует:

Траекторию движения тела (см. рис. 2.8) можно схематично представить небольшими участками наклонной плоскости, поэтому для, работы силы тяжести на всей траектории 1 -2 справедливо выражение

A 12 =mg (h 1 -h 2) =-(mg h 2 - mg h 1) (2.30)

Итак, работа силы тяжести не зависит от траектории тела, а зависит от различия в высотах расположения начальной и конечной точек траектории.

Величину

е п = mg h (2.31)

называют потенциальной энергией материальной точки (тела) массой m поднятой над землей на высоту h. Следовательно, формулу (2.30) можно переписать так:

A 12 = =-(En 2 - En 1) или A 12 = =-ΔEn (2.32)

Работа силы тяжести равна взятому с обратным знаком изменению потенциальной энергии тел, т. е. разности ее конечного и начального значений (теорема о потенциальной энергии ).

Подобные рассуждения можно привести и для упруго деформированного тела.

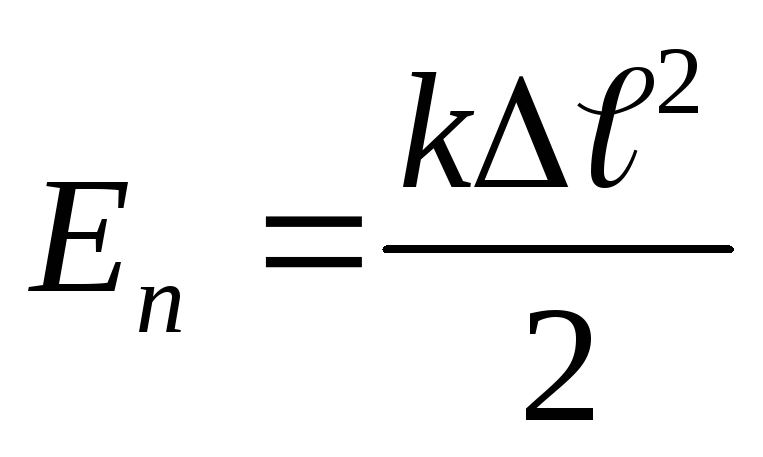(2.33)

Отметим, что физический смысл имеет разность потенциальных энергий как величина, определяющая работу консервативных сил. В связи с этим безразлично, какому положению, конфигурации, следует приписать нулевую потенциальную энергию.

Из теоремы о потенциальной энергии можно получить одно очень важное следствие: консервативные силы всегда направлены в сторону уменьшения потенциальной энергии. Установленная закономерность проявляется в том, что любая система, предоставленная самой себе, всегда стремится перейти в такое состояние, в котором её потенциальная энергия имеет наименьшее значение. В этом заключается принцип минимума потенциальной энергии .

Если система в данном состоянии не обладает минимальной потенциальной энергией, то это состояние называют энергетически невыгодным .

Если шарик находится на дне вогнутой чаши (рис.2.10,а), где его потенциальная энергия минимальна (по сравнению с ее значениями в соседних положениях), то его состояние более выгодно. Равновесие шарика в этом случае является устойчивым : если сместить шарик в сторону и отпустить, то он снова возвратится в своё первоначальное положение.

Энергетически невыгодным, например, является положение шарика на вершине выпуклой поверхности (рис.2.10, б). Сумма сил, действующих при этом на шарик, равна нулю, и потому, этот шарик будет находится в равновесии. Однако равновесие это является неустойчивым : достаточно малейшего воздействия, чтобы он скатился вниз и тем самым перешёл в состояние энергетически более выгодное, т.е. обладающее меньшей

потенциальной энергией.

При безразличном равновесии (рис. 2.10, в) потенциальная энергия тела равна потенциальной энергии всех его возможных ближайших состояний.

На рисунке 2.11 можно указать некоторую ограниченную область пространства (например cd), в которой потенциальная энергия меньше, чем вне её. Эта область получила название потенциальной ямы .

Кинетическая энергия поступательно движущегося твердого тела определяется очень просто. Так как все точки тела при таком движении имеют одинаковую скорость, то кинетическая энергия равна просто (4)

где - скорость тела, а М - его полная масса. Это выражение такое же, как если бы со скоростью двигалась одна материальная точка массы М. Ясно, что поступательное движение твердого тела вообще ничем существенным не отличается от движения материальной точки.

Определим теперь кинетическую энергию вращающегося тела. Для этого разделим его мысленно на отдельные элементарные части, настолько малые, чтобы их можно было считать движущимися как материальные точки. Если m i есть масса i-го элемента, а r i - его расстояние до оси вращения, то его скорость равна , где - угловая скорость вращения тела. Кинетическая энергия этого элемента равна и, просуммировав эти энергии, получим полную кинетическую энергию тела (5)

Стоящая здесь в скобках сумма зависит от того, с каким именно твердым телом мы имеем дело (от его формы, разме­ров и распределения масс в нем), а также от того, как расположена в нем ось вращения. Эта величина, характеризующая твердое тело и выбранную ось вращения, называется моментом инерции тела относительно данной оси.

Обозначим его буквой I: (6)

Если твердое тело - сплошное, то его нужно разделить на бесконечно большое количество бесконечно малых частей; суммирование в написанной формуле заменяется тогда интегрированием. Укажем для примера, что момент инерции сплошного шара (с массой М и радиусом R) относительно оси, проходящей через его центр, равен ; момент инерции тонкого стержня (длины l) относительно перпендикулярной ему оси, проходящей через его середи­ну, равен .

Таким образом, кинетическая энергия вращающегося тела может быть написана в виде (7)

Это выражение формально похоже на выражение для энергии поступательного движения, отличаясь от него тем, что вместо скорости V стоит угловая скорость , а вместо массы - момент инерции. Здесь мы имеем первый пример того, что при вращении момент инерции играет роль, аналогичную массе при поступательном движении.

Кинетическую энергию произвольно движущегося твердого тела можно представить в виде суммы поступательной и вращательной энергий, если в способе разделения двух движений выбрать основную точку О в центре инерции тела. Тогда вращательное движение будет представлять собой движение точек тела относительно его центра инерции, т.е.играет роль «внутреннего» движения. Поэтому для кинетической энергии произвольного движущегося тела имеем (8)

Индекс «0» у момента инерции означает, что он берется относительно оси, проходящей через центр инерции.

Рассмотрим твердое тело, вращающееся вокруг некоторой оси Z, не проходящей через центр инерции. Кинетическая энергия этого движения есть , где I - момент инерции относительно оси Z. С другой стороны, можно рассматривать это же движение как совокупность поступательного движения со скоростью V центра инерции и вращения (с той же угловой скоростью ) вокруг оси, проходящей через центр инерции параллельно оси Z. Если а есть расстояние центра инерции от оси Z, то его скорость V=a . Поэтому кинетическую энергию тела можно представить также и в виде

Сравнивая оба выражения, найдем

Эта формула связывает момент инерции тела относительно какой-либо, оси с моментом инерции относительно другой оси, параллельной первой и проходящей через центр инерции (теорема Гюйгенса-Штейнера). Очевидно, что I всегда больше, чем I 0 . Другими словами, при заданном направлении оси минимальное значение момента инерции достигается для оси, проходящей через центр инерции.

Кинети́ческая эне́ргия -скалярная функция, являющаяся мерой движения материальной точки и зависящая только отмассыимодуляскоростиматериальных точек, образующих рассматриваемую физическую систему ,энергиямеханической системы, зависящая отскоростейдвижения её точек в выбраннойсистеме отсчёта. Часто выделяют кинетическую энергиюпоступательногоивращательногодвижения.

Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия - частьполной энергии, обусловленнаядвижением .

Простым языком, кинетическая энергия - это энергия, которую телоимеет только при движении. Когдателоне движется, кинетическая энергия равна нулю.

Физический смысл

Рассмотрим систему, состоящую из одной частицы, и запишем второй закон Ньютона:

Есть равнодействующая всехсил, действующих на тело.Скалярно умножимуравнение наперемещениечастицы. Учитывая, что, получим:

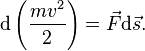
Если система замкнута, то есть внешние по отношению к системе силы отсутствуют, или равнодействующая всех сил равна нулю, то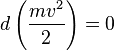, а величина

остаётся постоянной. Эта величина называется кинетической энергией частицы. Если система изолирована, то кинетическая энергия являетсяинтегралом движения.

Для абсолютно твёрдого телаполную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:

Масса тела

Скоростьцентра масстела

Момент инерциителакг·м²

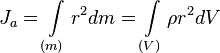
Угловая скоростьтела. рад/с

Найдем кинетическую энергию при различных случаях движения:

1. Поступательное движение

Скорости всех точек системы равны скорости центра масс . Тогда

Кинетическая энергия системы при поступательном движении равна половине произведения массы системы на квадрат скорости центра масс.

2. Вращательное движение (рис. 77)

Скорость любой точки тела: . Тогда

или используя формулу (15.3.1):

Кинетическая энергия тела при вращении равна половине произведения момента инерции тела относительно оси вращения на квадрат его угловой скорости.

3. Плоскопараллельное движение

При данном движении кинетическая энергия складывается из энергии поступательного и вращательных движений

Общий случай движения дает формулу, для вычисления кинетической энергии, аналогичную последней.

Определение работы и мощности мы сделали в параграфе 3 главы 14. Здесь же мы рассмотрим примеры вычисления работы и мощности сил действующих на механическую систему.

Физический смысл работы

Работавсех сил, действующих на частицу при её перемещении, идёт на приращение кинетической энергии частицы :

Свойства кинетической энергии

Аддитивность. Это свойство означает, что кинетическая энергия механической системы, состоящей из материальных точек, равна сумме кинетических энергий всех материальных точек, входящих в систему.

Инвариантность по отношению к повороту системы отсчета. Кинетическая энергия не зависит от положения точки, направления её скорости и зависит лишь от модуля скорости или, что то же самое, от квадрата её скорости.

Сохранение. Кинетическая энергия не изменяется при взаимодействиях, изменяющих лишь механические характеристики системы.Это свойство инвариантно по отношению к преобразованиям Галилея Свойства сохранения кинетической энергии и второго закона Ньютона достаточно, чтобы вывести математичекую формулу кинетической энергии.

Релятивизм

При скоростях, близких к скорости света, кинетическая энергия любого объекта равна

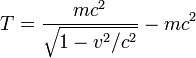
Массаобъекта;

Скоростьдвижения объекта в выбранной инерциальной системе отсчета;

Скорость светав вакууме (-энергия покоя).

Данную формулу можно переписать в следующем виде:

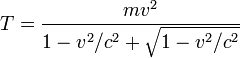
При малых скоростях () последнее соотношение переходит в обычную формулу.

Соотношение кинетической и внутренней энергии

Кинетическая энергия зависит от того, с каких позиций рассматривается система. Если рассматривать макроскопический объект (например, твёрдое тело видимых размеров) как единое целое, можно говорить о такой форме энергии, как внутренняя энергия. Кинетическая энергия в этом случае появляется лишь тогда, когда тело движется как целое.

То же тело, рассматриваемое с микроскопической точки зрения, состоит из атомовимолекул, и внутренняя энергия обусловлена движением атомов и молекул и рассматривается как следствиетеплового движенияэтих частиц, а абсолютная температура тела прямо пропорциональна средней кинетической энергии такого движения атомов и молекул. Коэффициент пропорциональности -Постоянная Больцмана.